引论
在几何学中,平面交叉是指两个平面的重叠部分。判断两个平面是否相交是一个重要的概念,应用于工程、建筑和计算机图形等许多领域。本文将探讨两个平面交叉的条件,并对交叉后的几何特征进行深入分析。
相交条件
两个平面交叉的充分必要条件是:
平行条件:如果两个平面是平行的(即它们没有公共点),它们就不会相交。
共线条件:如果两个平面包含相同的直线,则它们相交。
几何特征
当两个平面相交时,它们形成一条交线,即两个平面重叠的直线。交线具有以下几何特征:
垂直:交线垂直于两平面。
共点:交线上的所有点都属于两个平面。
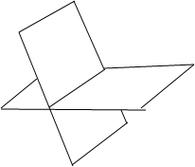
分隔:交线将两个平面分成两个半空间。
确定相交线
通过以下方法确定两个平面交叉的交叉线:
平面法:找到包含两个平面的第三个平面,然后确定第三个平面与两个原平面的交叉线。交叉线将是原平面的交叉线。
向量法:用两平面法向量求解交线的参数方程。
应用
在许多实际应用中,平面相交的概念非常重要,包括:
建筑:确定建筑墙壁、屋顶和地板之间的交叉线,以确保结构的稳定性。
工程:设计管道、桥梁和其它结构,确保它们能够在交叉处正确连接。
计算机图形学:渲染三维场景,需要计算不同平面之间的交线,以产生逼真的图像。
两个平面交叉的条件和几何特征是理解平面几何的基础。设计复杂结构或创建三维模型等实际问题可以通过理解和应用这些概念来解决。本文为读者提供了对平面交叉的全面理解,这对各种几何和应用领域至关重要。