在几何的宏伟世界中,圆柱面相交的现象是一个令人叹为观止的课题。它不仅挑战我们的空间想象力,还揭示了数学与现实世界之间的奇妙联系。当两个圆柱面交汇时,形成的图形既复杂又美丽,令人不禁好奇这些几何形状如何在三维空间中相互交织。本文将深入探讨这一现象,揭示其中的数学原理和几何美学。
让我们回顾一下圆柱面的基本概念。圆柱面是一个由无限多条平行的直线沿着一个固定的曲线生成的表面。这些直线与曲线保持一定的距离,使得圆柱面在空间中具有独特的几何性质。圆柱面可以看作是三维空间中的扩展曲面,其截面常常是圆形。
当两个圆柱面相交时,它们的交线构成了一系列复杂的几何图形。具体来说,两个圆柱面的交线通常呈现为一组曲线,这些曲线的形状和数量取决于圆柱面之间的相对位置和角度。交线的形状可能是双曲线、椭圆或抛物线,这取决于圆柱面的参数。通过精确的数学计算和几何分析,我们可以揭示这些曲线的详细特征,从而深入了解圆柱面相交的本质。
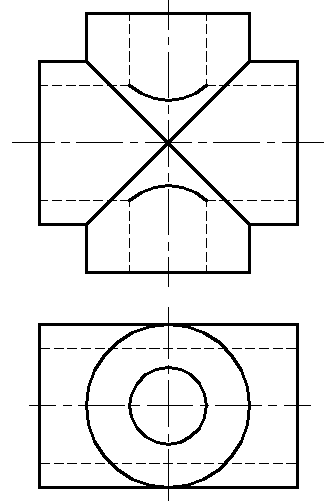
要详细了解圆柱面相交的图形,我们需要从数学上进行解析。设定两个圆柱面的方程,并将它们代入联立方程中,可以得到它们的交线方程。这些方程通常比较复杂,但通过代数和几何方法,我们可以解出交线的具体方程。这些方程的解反映了圆柱面相交时产生的几何图形的性质,如曲线的类型和位置。通过这些数学分析,我们能够揭示交线的详细特征,从而深入理解这一几何现象。
圆柱面相交的现象不仅仅存在于抽象的数学世界中,它在工程和设计中也有着广泛的应用。在建筑设计中,圆柱面相交的图形常常被用来创造独特的视觉效果和结构功能。工程师们利用这些几何原理来设计复杂的结构,如拱形桥梁和高耸的摩天大楼。在这些应用中,了解圆柱面相交的几何特性可以帮助设计师和工程师优化结构的稳定性和美观性。
两个圆柱面相交的现象展示了几何学的丰富多彩和复杂性。从基本概念到数学解析,再到实际应用,这一现象不仅令人着迷,也具有广泛的实际意义。深入研究这些交汇现象,可以帮助我们更好地理解空间几何的奥秘,并在实际应用中发挥重要作用。未来,随着数学和工程技术的不断发展,我们将有更多机会深入探索这一领域的潜力和应用。