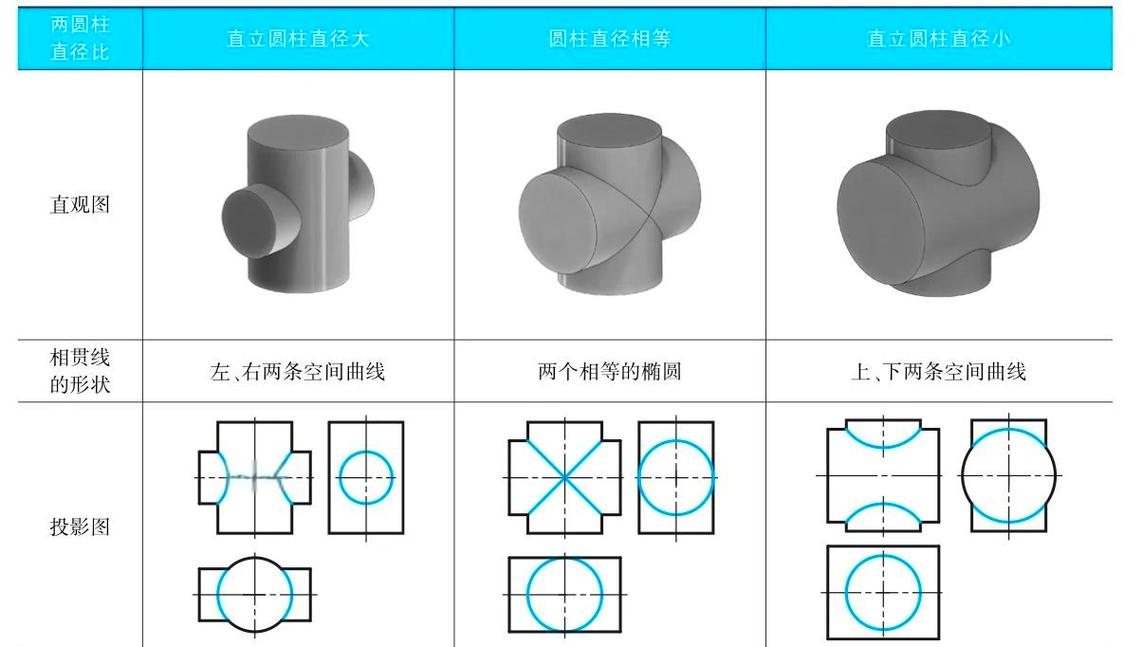
定义
机械表面相贯线是指两个表面相交的曲线,两个表面都位于同一位置。一般来说,这是两个表面相遇形成的边界线。
计算
相贯线的计算涉及以下步骤:
获取曲面方程:获取描述两个曲面的方程或参数方程。
建立隐式方程:将两个曲面方程连接起来,消除参数,得到相贯线方程。
求解交点:用代数或数值方法求解相贯线方程的交点。
应用
相贯线广泛应用于机械设计,如:
1. 齿轮齿廓设计:齿轮齿廓是相贯线的典型应用,它决定了齿轮的啮合性能。
2. 凸轮设计:凸轮与从动件之间形成的相贯线描述了从动件的运动轨迹。
3. 轴承表面设计:轴承中的滚子或球体与轴承内圈或外圈形成的相贯线影响轴承的载荷分布和使用寿命。
4. 流体动力学:在流体流动分析中,相贯线用于表示不同流体的分界面或物体与流体的边界。
案例分析
行星齿轮传动
在行星齿轮传动中,行星齿轮与内齿圈和太阳齿轮形成三条相贯线。这三条相贯线共同决定了行星齿轮的啮合状态和传动比。
计算步骤:
内齿圈方程:x^2 y^2 = R^2
太阳齿轮方程:x^2 y^2 = r^2
相贯线方程:x^2 y^2 = R^2 - r^2
交点:(-R r, 0), (-R - r, 0)
相贯线的意义
行星齿轮传动中的相贯线决定了行星齿轮的啮合点,从而影响传动效率和噪声水平。优化相贯线的形状可以提高传动性能。
相贯线是机械设计中的一个重要概念,它连接两个相交表面,影响产品的性能。优化机械系统设计,了解相贯线的计算和应用至关重要。